A fortran library for numerical integration with dense output and multiple event-detection support. Currently, it provides four Explicit Runge-Kutta methods: DOP54, DOP853, Verner65E, and Verner98R.
- Version
- 0.9.9
- Date
- Created: 01/25/2019
- Copyright
- Copyright 2024 Bharat Mahajan
The initial code was written by Bharat Mahajan at Odyssey Space Research LLC, Houston, TX as part of the work under contract no. 80JSC017D0001 with NASA-Johnson Space Center. FLINT source code is licensed under the Apache License, Version 2.0 (the "License") found in LICENSE file contained in this distribution.
The coefficients for DOP853 method were derived by Ernest Hairer. His original codes are available at http://www.unige.ch/~hairer/software.html. The coefficients for Verner65E and Verner98R methods were derived by Jim Verner, and are available at http://people.math.sfu.ca/~jverner/.
Introduction
FLINT is a modern object-oriented Fortran library that provides four adaptive step-size explicit Runge-Kutta (ERK) methods of order 5, 6, 8, and 9 along with dense-output and multiple event-detection support for each of the methods. The code is written such that any other ERK method can be implemented by including its coefficients with minimum changes required in the code. The DOP54 and DOP853 integrators step implementation is hand-optimized and for other integrators, a generic routine for step integration enables quick inclusion of new ERK methods. This generic step integration routine supports both FSAL and non-FSAL methods. Dense output is supported with delayed interpolation. When interpolation is enabled, FLINT computes the interpolation coefficients during the integration and stores them in internal memory. Thereafter, the interpolation method can be used any number of times to find the solution values at any user-specified grid within the initial and final conditions. Interpolation is performed much faster than integration as the coefficients are all precomputed during the integration. Multiple event detection is supported for each integrator along with many features such as event root-finding, event step-size, event actions. In a nutshell, the features are:
- Modern object-oriented, thread-safe, and optimized Fortran code
- 4 Adaptive-step ERK integrators: DOP54, DOP853, Verner98R, Verner65E
- Fixed step size for integration is supported as well as the ability to propagate for a single step and return control to the user
- Any other ERK method can be implemented by including their coefficients
- Dense output with delayed interpolation (integrate once, interpolate as many times)
- Multiple event-detection as well as finding location of events using root-finding
(Brent's algorithm) with static and dynamic event masking - Ability to set a maximum delay (referred to here as event step-size) after which events are guaranteed to be detected
- Ability to restart the integration or change solution on the detection of events
- Stiffness detection
The following figure shows the multiple event detection capability of FLINT, in which the X-crossings in decreasing and Y-crossings in increasing directions of a three-body orbit are detected by FLINT.
Introduction
The latest FLINT code (compiled using Intel Fortran compiler ifort) is tested against Julia's (ver 1.10.0) DifferentialEquations package ver 7.12.0 (https://diffeq.sciml.ai/stable/) for different problems with and without event detection. The Julia test code along with results are provided in the tests folder in FLINT's GitHub repository https://github.com/princemahajan/FLINT. Benchmark charts are provided in the media folder.
- Work-Precision Data for Three-Body problem (No events)
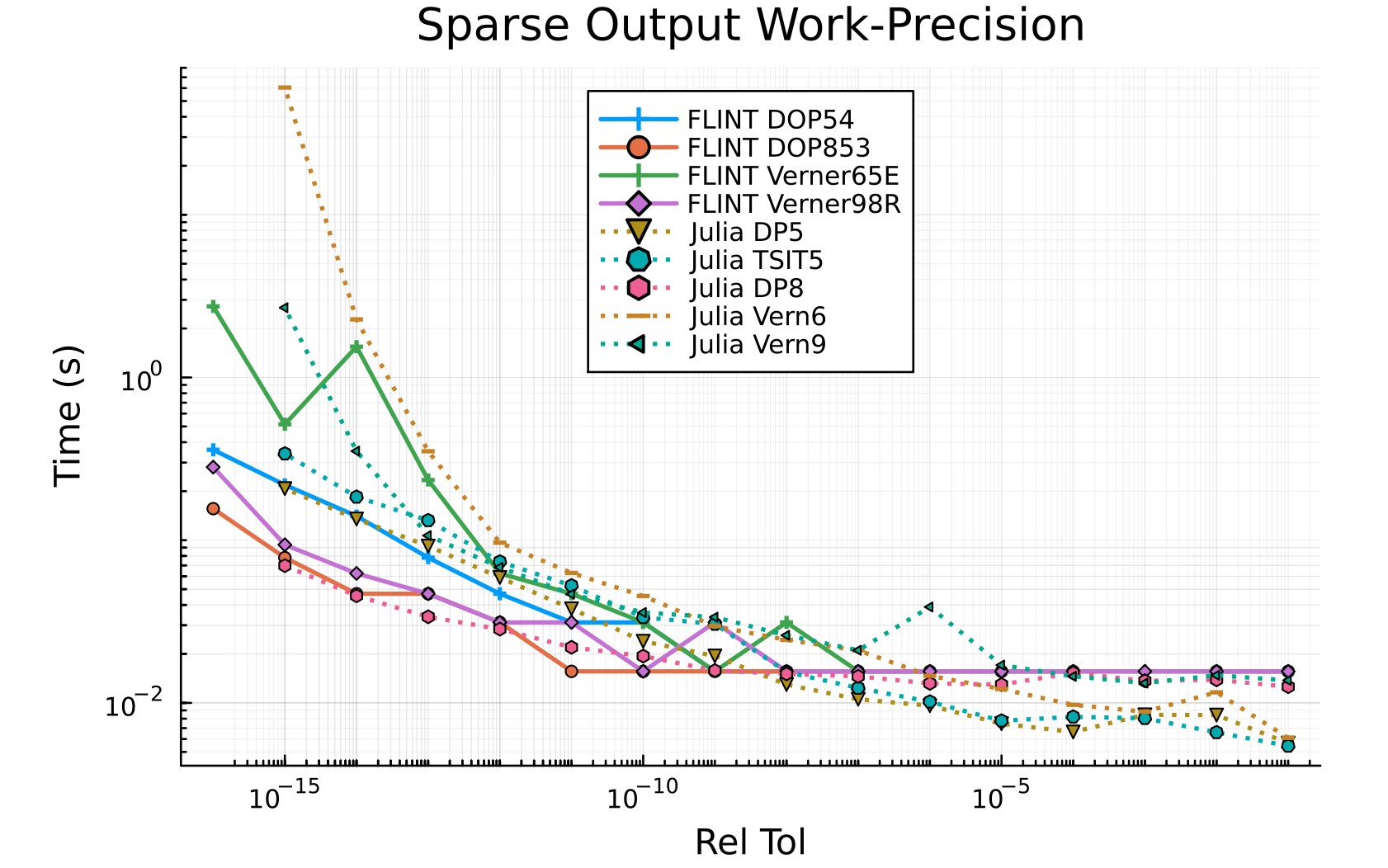
- Three-Body problem propagation
- Lorenz equations integration
For all the FLINT status codes and options supported by Init, Integrate, and Interpolate procedures along with the interfaces for user-supplied functions, see the docs and/or FLINT_base module at https://github.com/princemahajan/FLINT/blob/master/src/FLINT_base.f90).
References
- Hairer, Ernst, Norsett, Syvert P., Wanner, Gerhard, Solving Ordinary Differential Equations I, Springer-Verlag Berlin Heidelberg, 2nd Ed., 1993.